Geometría y aspectos operativos de los modos simples de propagación ionosférica
Principal → Artículos Técnicos → Geometría y aspectos operativos de los modos simples de propagación ionosférica |
![]() This article is also available in English (este artículo también está disponible en inglés).
This article is also available in English (este artículo también está disponible en inglés).
![]() Resumen:
Resumen:
En este artículo se describe la geometría de la propagación de las ondas de radio a través de sucesivos saltos y utilizando a alguna de las capas de la ionosfera como reflector, modalidad típica de la banda de HF y bajo determinadas condiciones también de la banda de VHF o incluso de la de UHF.
Para simplificar el análisis, se considera la teoría de rayos rectos y reflexión pura, es decir, los rayos no están afectados por refracción ni dispersión a lo largo de todo el trayecto radioeléctrico. Como primera aproximación, se tratarán solamente los modos de propagación simples, en los que interviene una unica capa de la ionosfera como reflector.
Para determinar si un enlace por reflexión ionosférica es factible, hemos de considerar tres grandes cuestiones.
La primera de ellas es la geometría del enlace, que determina en qué zonas de la Tierra vamos a tener cobertura y en qué zonas de la ionosfera se producen las reflexiones.
La segunda es el balance de potencias, en el que entran en juego las características técnicas de los equipos y las antenas utilizados, como la potencia de transmisión, la ganancia de las antenas, las pérdidas de las líneas de transmisión o la sensibilidad del receptor. Tendremos además atenuaciones adicionales debidas a la propagación de las ondas y a su reflexión tanto en la ionosfera como en la superficie terrestre. El cómputo total ha de ser suficiente para que el receptor pueda demodular las señales procedentes del transmisor.
Y finalmente también hemos de considerar la frecuencia de trabajo, que para un determinado circuito ha de ser siempre
inferior a la máxima frecuencia utilizable o MUF.
1. Análisis para un único salto.
Para estudiar la geometría de un enlace radio ionosférico, podemos realizar en primer lugar el análisis de la geometría de un único salto y después extrapolar los resultados. Para ello, nos apoyaremos en la figura 1.
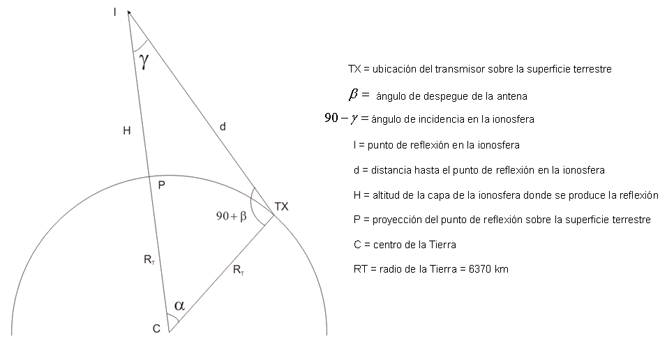
Fig.1. Geometría de un salto ionosférico
Son datos conocidos:
-
La ubicación del transmisor sobre la superficie terrestre.
-
El ángulo de despegue de la antena. Si es igual a cero, la antena está apuntanto al horizonte.
-
La altitud de la capa de la ionosfera donde se produce la reflexión.
-
El radio de la Tierra (unos 6370 km).
Las reflexiones en la ionosfera se producen a altitudes aproximadas de 100 km para el caso de las capas E y E esporádica y a unos 300 km para el caso de la capa F.
Los enlaces que utilizan una sola capa de la ionosfera como reflector determinan los modos de propagación simples, que se denominan con un número que indica el número de saltos, junto a la letra que identifica a la capa en la que se ha producido la reflexión.
De esta forma, el modo de propagación que utiliza un salto en la capa F se denomina 1F, si hay dos saltos en esa capa el modo se denomina 2F y así sucesivamente. Para "n" saltos podemos generalizar hablando de modos "nF".
Lo mismo sucede si las reflexiones se producen exclusivamente en la capa E: para "n" saltos, hablaremos de modos "nE".
2. Longitud del trayecto radioeléctrico.
Determinar la longitud del trayecto radioeléctrico nos servirá para determinar las pérdidas de propagación y la distancia de cada salto.
En un único salto, la onda de radio recorrerá dos veces la distancia "d": una vez entre el transmisor "TX" y el punto "I" de la ionosfera y otra vez entre dicho punto y la superficie terrestre.
Para calcular "d", identificando el triángulo formado por los puntos "TX-I-C", utilizaremos el teorema del coseno:
| [1] |
Si desarrollamos el término de la izquierda en [1], resulta la siguiente ecuación de segundo grado [2], siendo "d" la incógnita:
| [2] |
La solución de esta ecuación es [3]:
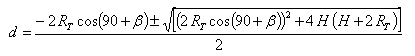 |
[3] |
Es decir, podemos determinal la distancia "d" a partir del radio terrestre, el ángulo de despegue de la antena y la altitud a la que se produce la reflexión en la ionosfera.
3. Distancia de salto.
La distancia de salto será el doble de la longitud del arco de superficie terrestre comprendido entre los puntos "TX" y "P". La longitud del arco viene dada por:
| [4] |
Para determinar dicha distancia, resulta necesario conocer previamente el valor del ángulo alfa, expresado en grados. Para ello, podemos aplicar el teorema del seno al triángulo formado por los puntos "TX-I-C", que tendrá la siguiente formulación:
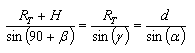 |
[5] |
Si en [5] consideramos el primer y el último término, despejando resulta:
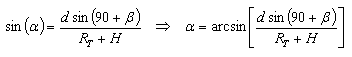 |
[6] |
Donde la distancia "d" entre los puntos "TX" e "I" ha sido calculada previamente en [3].
Por tanto, combinando [4] y [6], la distancia de salto resulta ser:
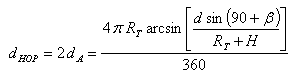 |
[7] |
Es decir, la distancia de salto puede determinarse a partir del radio de la Tierra, el ángulo de despegue de la antena, la altitud de la capa de la ionosfera en la que se produce la reflexión y la distancia desde la estación transmisora hasta el punto de reflexión en la ionosfera.
4. Zonas de cobertura.
Una vez conocido el método para calcular las distancias de salto, podemos determinar las zonas de cobertura que tendrá el transmisor trabajando con un ángulo de despegue determinado y usando una capa concreta de la ionosfera como reflector.
En este apartado el análisis será exclusivamente geométrico. Será necesario complementarlo a posteriori con un análisis del balance de potencias para ver si los enlaces radio son posibles con cada una de las zonas de cobertura determinadas.
En cada salto, la distancia máxima se consigue con un ángulo de despegue nulo, es decir, con las antenas apuntando al horizonte, o lo que es lo mismo, con un trayectoria radioeléctrica tangente a la superficie terrestre.
No obstante, el diagrama de radiación de una antena directiva presenta un ancho de haz a -3 dB que no debemos despreciar, por lo que es común considerar que en esas circunstancias la antena radia con ángulos de despegue comprendidos entre 0º y 2º.
El rayo que sale a 2º se reflejará en la ionosfera con un ángulo de incidencia mayor que el que sale a 0º, por lo que acabará reflejándose de nuevo en la superficie terrestre a una distancia menor que el rayo que sale a 0º. Estudiaremos por tanto los dos rayos que delimitan la radiación de la antena. El rayo que sale a 0º determinará el alcance máximo y el que sale a 2º el alcance mínimo en cada uno de los saltos, alcances que pueden calcularse aplicando la fórmula [7].
Por otro lado, también podemos calcular a qué distancias del transmisor se produce la reflexión ionosférica en cada caso, aplicando para ello la fórmula [4].
En la figura 2, el rayo a 0º está coloreado en azul y el rayo a 2º en rojo, representándose con un modelo plano tanto la superficie terrestre como la ionosfera. La escala se ha exagerado para que la representación pueda interpretarse con más claridad.
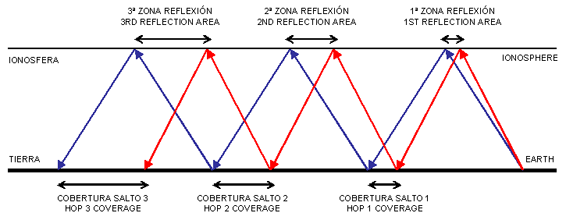
Fig.2. Cobertura de los saltos sucesivos
Como puede apreciarse en la fig.2, el efecto de la diferencia de ángulos de incidencia de los dos rayos provoca que las zonas de cobertura de cada salto vayan siendo cada vez más amplias, conforme avanza el frente de ondas.
Si suponemos que la reflexión se está produciendo en la capa E o en la capa E esporádica de la ionosfera, a una altitud de 100 km, geométricamente tendremos las zonas de cobertura que se muestran en la tabla 1.
| Salto | Distancia mínima (km) | Distancia máxima (km) |
|---|---|---|
| 1 | 1841 | 2243 |
| 2 | 3683 | 4486 |
| 3 | 5524 | 6728 |
| 4 | 7365 | 8971 |
| 5 | 9207 | 11214 |
Tabla 1. Zonas de cobertura en los modos nE
Para esos mismos modos nE, en la tabla 2 se muestran las zonas en las que se producirán las reflexiones ionosféricas.
| Salto | Distancia mínima (km) | Distancia máxima (km) |
|---|---|---|
| 1 | 921 | 1121 |
| 2 | 2762 | 3364 |
| 3 | 4603 | 5607 |
| 4 | 6445 | 7850 |
| 5 | 8286 | 10093 |
Tabla 2. Zonas de reflexión ionosférica en los modos nE
Si ahora suponemos que la reflexión se está produciendo en la capa F, a una altitud de 300 km, geométricamente tendremos las zonas de cobertura que se muestran en la tabla 3.
| Salto | Distancia mínima (km) | Distancia máxima (km) |
|---|---|---|
| 1 | 3416 | 3836 |
| 2 | 6831 | 7671 |
| 3 | 10247 | 11507 |
| 4 | 13663 | 15342 |
| 5 | 17079 | 19178 |
Tabla 3. Zonas de cobertura en los modos nF
Para esos mismos modos nF, en la tabla 4 se muestran las zonas en las que se producirán las reflexiones ionosféricas.
| Salto | Distancia mínima (km) | Distancia máxima (km) |
|---|---|---|
| 1 | 1708 | 1918 |
| 2 | 5124 | 5753 |
| 3 | 8539 | 9589 |
| 4 | 11955 | 13424 |
| 5 | 15371 | 17260 |
Tabla 4. Zonas de reflexión ionosférica en los modos nF
Dado que la altitud a la que se produce la reflexión ionosférica es mayor, cada salto de los modos nF es más largo que cada salto de los modos nE. Como ventaja adicional de los modos nF sobre los modos nE, para una misma distancia de enlace la onda de radio atraviesa menos veces la capa D de la ionosfera, donde existen elevados índices de atenuación por absorción.
En todos los casos, las distancias pueden ser distintas en función de la altitud exacta a la que se produce la reflexión ionosférica, por lo que los datos de las tablas han de considerarse orientativos.
Los datos obtenidos pueden representarse en aplicaciones y sistemas de información geográfica, como Google Earth, que permiten comprobar de forma visual con qué zonas se tendrá cobertura en cada modo. En la fig.3 se muestra un ejemplo de la cobertura aproximada proporcionada por los modos nE desde las Islas Canarias (EA8).
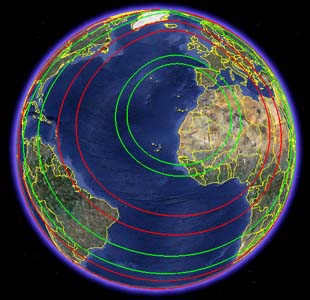
Fig.3. Cobertura de los modos nE desde las Islas Canarias
5. Balances de potencia.
Se denomina balance de potencias al resultado de aplicar la ecuación de propagación a un enlace radio. Para calcularlo, nos apoyaremos en el esquema mostrado en la fig.4.
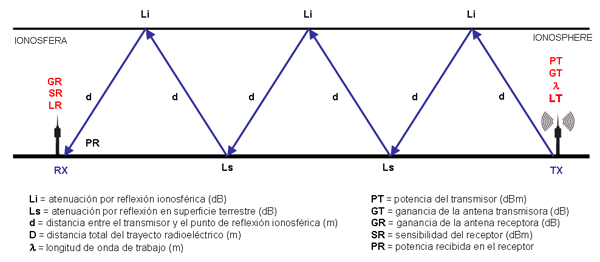
Fig.4. Parámetros de la ecuación de propagación
La ecuación de propagación viene dada por:
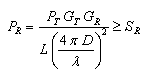 |
[8] |
Es decir, en el extremo del receptor, la potencia recibida ha de ser superior a la sensibilidad del receptor para que el enlace radio sea posible.
Cuentan a favor del enlace la potencia de transmisión y la ganancia de las antenas transmisora y receptora.
En contra del enlace cuentan la atenuación en espacio libre (el término entre paréntesis al cuadrado en el denominador de [8]) y otros factores de atenuación, como la propia de las líneas de transmisión y los conectores tanto en el transmisor como en el receptor y la atenuación que sufre la onda en cada reflexión en la ionosfera ("Li") o en la superficie terrestre ("Ls"). Todos los factores de atenuación indicados, salvo el relativo al espacio libre, se agrupan bajo el término "L" en la ecuación [8].
La atenuación debida a las reflexiones ionosféricas y en la superficie terrestre es muy dificil de evaluar, ya que depende de factores como la densidad de ionización de las capas ionosféricas o la conductividad del medio donde se producen las reflexiones en la superficie terrestre. Por ejemplo, si la onda se refleja en el mar, la atenuación será mucho menor que si se refleja en tierra.
Podemos hacer una aproximación muy general de esos niveles de atenuación, considerando que en cada reflexión en la
ionosfera se tiene una atenuación "Li" de 5 dB en el primer salto, 5 dB en el segundo salto, 3,5 dB en el tercer salto
y 2,5 dB por cada uno de los saltos sucesivos. Para las reflexiones en la superficie terrestre, introduciremos unas
pérdidas adicionales "Ls" de 3,5 dB por cada salto.
La distancia "D" en [8] es la longitud total del trayecto radioeléctrico, igual a la suma de todos los tramos de longitud "d" indicados en la fig.4 y cuyo valor puede calcularse con [3].
Si expresamos la ecuación de propagación [8] en forma logarítmica, resulta [9]:
| [9] |
Una vez calculada la potencia recibida y conocida la sensibilidad de nuestro receptor, el margen de desvanecimiento o
margen de fading se define como [10]:
| [10] |
Si el margen de fading es positivo, el enlace es posible y su valor es precisamente el número de dB extras que tenemos
disponibles para afrontar atenuaciones adicionales del enlace, como por ejemplo la propagación multitrayecto o la
absorción causada por las tormentas geomagnéticas. Si el margen de fading es negativo, el nivel de señal recibida está por debajo
de la sensibilidad de nuestro receptor y por tanto esa señal no se puede demodular.
Pongamos como ejemplo un enlace ionosférico con las siguientes características:
-
Frecuencia de trabajo en la banda de 7 MHz (40 metros).
-
Potencia de transmisión de 100 W (50 dBm).
-
Antenas apuntando al horizonte, con ganancias de 7 dBi tanto en el transmisor como en el receptor.
-
Sensibilidad del receptor de -123 dBm.
-
Pérdidas adicionales debidas al cableado y conectores de 1 dB tanto en el transmisor como en el receptor.
Podemos analizar los márgenes de fading que tendremos disponibles en los diferentes modos nE y nF.
Para cada modo, en primer lugar determinamos la longitud total del trayecto radioeléctrico ("D"), empleando para ello
la fórmula [3]. Consideraremos que las reflexiones en la capa E se producen a una altitud de 100 km y las reflexiones
en la capa F a una altitud de 300 km.
Considerando el número de reflexiones que se producen en cada modo y con los valores teóricos de "Li" y "Ls" expuestos, podemos calcular la atenuación total "L" del circuito radioeléctrico. Con la fórmula [9] podemos calcular la potencia recibida y con la fórmula [10] el margen de fading.
Los resultados para los modos nE se muestran en la tabla 5.
| Modo | Distancia trayecto (km) | Potencia recibida (dBm) | Margen fading (dB) |
|---|---|---|---|
| 1E | 2266 | -64 | 58 |
| 2E | 4533 | -73 | 49 |
| 3E | 6799 | -84 | 38 |
| 4E | 9065 | -92 | 30 |
| 5E | 11331 | -100 | 22 |
Tabla 5. Balances de potencia en los modos nE
Los resultados para los modos nF se muestran en la tabla 6.
| Modo | Distancia trayecto (km) | Potencia recibida (dBm) | Margen fading (dB) |
|---|---|---|---|
| 1F | 3956 | -69 | 53 |
| 2F | 7912 | -78 | 44 |
| 3F | 11867 | -89 | 33 |
| 4F | 15823 | -97 | 25 |
| 5F | 19779 | -105 | 17 |
Tabla 6. Balances de potencia en los modos nF
Insistir nuevamente en que los valores son orientativos, por los motivos anteriormente expuestos.
6. Máxima frecuencia utilizable.
La URSI define la máxima frecuencia utilizable (MUF) como "la máxima frecuencia para transmisión ionosférica usando una trayectoria oblícua, para un sistema determinado".
La MUF depende de factores como la altitud a la que se produce la reflexión de las ondas, la densidad de ionización existente en ese punto o el ángulo de incidencia de la onda de radio en la ionosfera.
En la práctica, podemos determinar la MUF gracias a los datos ofrecidos por las estaciones de sondeo ionosférico, también conocidas como ionosondas. Las ionosondas están constantemente realizando mediciones que permiten determinar, entre otros parámetros, la altitud y el espesor de cada capa de la ionosfera y su frecuencia crítica. Estos datos se plasman en unas gráficas denominadas ionogramas.
La frecuencia crítica (fo) es la máxima frecuencia que una onda de radio transmitida perpendicularmente hacia la ionosfera puede tener para que dicha onda se refleje de vuelta hacia la superficie terrestre. Cada capa de la ionosfera tiene su propia frecuencia crítica, que varía con la hora del día: foE para la capa E, foEs para la capa esporádica Es, foF2 para la capa F2, etc.
Para el caso de España, disponemos de dos estaciones de sondeo ionosférico con datos públicos:
Los ionogramas de ambas ionosondas pueden consultarse en tiempo real en el Panel de HF.
En la figura 5 se muestra un ejemplo de ionograma de la estación del Observatorio del Ebro, obtenida el 22/04/2010 a las 16:30 UTC. En la parte izquierda podemos ver que la frecuencia de corte de la capa F2 para esa hora es foF2 = 6.525 MHz.
Fig.5. Ionograma del Observatorio del Ebro obtenido el 22/04/2010 a las 16:30 UTC
Conocida la fo de una capa ionosférica y apoyándonos de nuevo en el esquema de la fig.1, su MUF puede calcularse mediante la siguiente fórmula [11]:
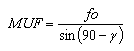 |
[11] |
Es decir, para una determinada capa de la ionosfera, la máxima frecuencia utilizable es igual al cociente entre la frecuencia crítica y el seno del ángulo de incidencia de la onda de radio en dicha capa.
Para determinar el ángulo de incidencia en la ionosfera, cuyo seno aparece en el denominador de [11], dado que conocemos el ángulo de elevación de nuestra antena y que podemos calcular el ángulo alfa con la fórmula [6], sabiendo que en cualquier triángulo la suma de sus ángulos es igual a 180º, resulta [12]:
| [12] |
Con este valor y la fo medida por la ionosonda, podemos calcular la MUF de nuestro circuito si la reflexión ionosférica
se produce en una zona cercana a la ionosonda. Para reflexiones múltiples, hemos de esperar que en cada punto de reflexión
ionosférica la fo sea distinta, debido por ejemplo a que un circuito puede atravesar zonas de día y zonas de noche en
las que la densidad de ionización es distinta. Para estos casos, calculada la MUF en cada punto, la MUF resultante será
la mínima de todas ellas.
Observando los datos ofrecidos por una ionosonda, concretamente el valor de las frecuencias de corte de cada capa, podemos preguntarnos si esos valores son suficientes para permitirnos trabajar en una banda determinada. Por ejemplo, comprobamos que una ionosonda detecta la presencia de la capa E esporádica y mide su frecuencia de corte foEs. ¿Será esa foEs suficiente para permitirnos trabajar, por ejemplo, en la banda de 50 MHz?.
Si en [11] prefijamos una MUF mínima necesaria para cada banda, por ejemplo de 50 MHz, 144 MHz ó 430 MHz y calculamos con [12] el ángulo de incidencia en la ionosfera correspondiente a cada altitud de reflexión en la ionosfera, con las antenas apuntando al horizonte, podemos obtener las gráficas que se muestran a continuación. Para cada altitud indicada, el punto de reflexión en la ionosfera se encontrará cada vez más lejos del transmisor.
La gráfica de la fig.6 muestra la fo necesaria para tener una MUF que permita trabajar en la banda de 50 MHz (6 m).
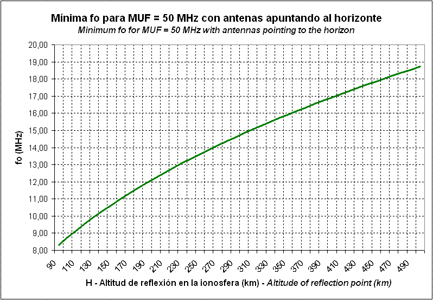
Fig.6. Mínima fo necesaria para trabajar en 50 MHz
La gráfica de la fig.7 muestra la fo necesaria para tener una MUF que permita trabajar en la banda de 144 MHz (2 m).
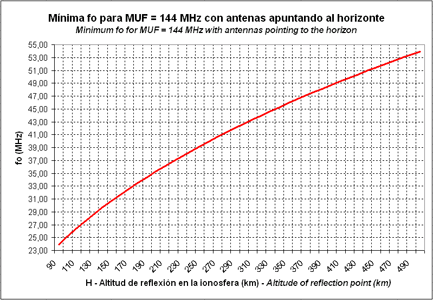
Fig.7. Mínima fo necesaria para trabajar en 144 MHz
Y finalmente, la gráfica de la fig.8 muestra la fo necesaria para tener una MUF que permita trabajar en la banda de 430 MHz (70 cm).
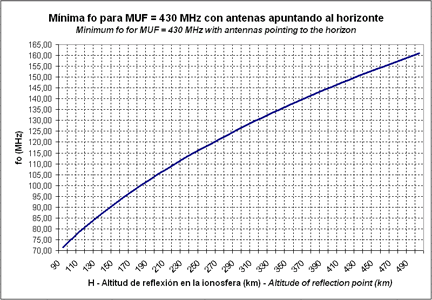
Fig.8. Mínima fo necesaria para trabajar en 430 MHz
Por ejemplo, queremos conocer la mínima frecuencia de corte de la capa E esporádica, medida por la ionosonda, que nos permita trabajar a 50 MHz. Si la capa esporádica E se ubica a una altitud de 100 km, consultando la gráfica de la fig.6 comprobamos que ha de tener una foEs mínima de 8,76 MHz. Si quisiéramos trabajar la esporádica E a 144 MHz, la foEs mínima debería ser de 25,22 MHz (fig.7) y a 430 MHz debería ser de 75,31 MHz (fig.8).
El pasado 22 de abril de 2010 se registró una apertura en 50 MHz entre las 16:30-17:30 UTC, permitiendo enlaces entre EA y
otros países como DL, SP y OK. Si observamos nuevamente el ionograma de la figura 4, correspondiente a ese mismo
horario, comprobamos que la frecuencia de corte de la capa esporádica E era foEs = 7,60 MHz. Aunque no llega al
valor mínimo de 8,76 MHz, si es indicador de una capa E esporádica de ionización alta, que en las zonas en las
que se produjo la reflexión ionosférica (más al norte, con foEs mayor) fue suficiente para posibilitar los enlaces.
Por tanto, los datos de las ionosondas son un buen indicador de las aperturas de propagación en cada banda.
7. Conclusiones.
Los modos simples de propagación ionosférica son aquellos en los que se utiliza una sola capa de la ionosfera para establecer los enlaces radio, normalmente la E, la E esporádica o la F. Operativamente, cada modo viene definido por la geometría del enlace, el balance de potencias y la máxima frecuencia utilizable.
El estudio de la geometría del enlace nos permite determinar en qué zonas de la ionosfera se producen las reflexiones y en qué zonas de la superficie terrestre existirá cobertura. Estos datos pueden calcularse a partir del ángulo de elevación de las antenas, el radio terrestre y la altitud a la que se produce la reflexión.
Para el cálculo del balance de potencias han de tenerse en cuenta la longitud del trayecto radioeléctrico, la frecuencia de trabajo, la potencia de transmisión, la atenuación de las líneas de transmisión y la sensibilidad del receptor. Las pérdidas inherentes a la propagación ionosférica, que se producen por la absorción y la reflexión, son dificiles de cuantificar pero pueden aproximarse por valores teóricos. El resultado del balance de potencias nos indicará el margen de fading disponible para trabajar.
Finalmente, la máxima frecuencia utilizable puede determinarse con la ayuda de los ionogramas ofrecidos por las estaciones de sondeo ionosférico, conocidas las frecuencias críticas de cada capa y el ángulo de incidencia de las ondas de radio en las mismas. El análisis de los ionogramas nos permite además determinar en qué momentos se están produciendo aperturas en cada banda. En este artículo se proporcionan gráficas para ayudar a detectar aperturas en 50 MHz, 144 MHz y 430 MHz a partir de los ionogramas.
Ismael Pellejero - EA4FSI |

